扇形|落点_Flutter绘制探索|扇形区域与点击校验

篇首语：本文由编程笔记#小编为大家整理，主要介绍了Flutter 绘制探索 | 扇形区域与点击校验相关的知识，希望对你有一定的参考价值。

作者&＃xff1a;张风捷特烈
链接&＃xff1a;https://juejin.cn/post/7158978916122624013

0. 前言

今天来探索一个问题&＃xff0c;如何绘制一块扇形区域路径&＃xff0c;并且校验触点是否落在 扇形区域 之中。这个问题对于绘制 饼图 及处理手势事件校验非常重要。

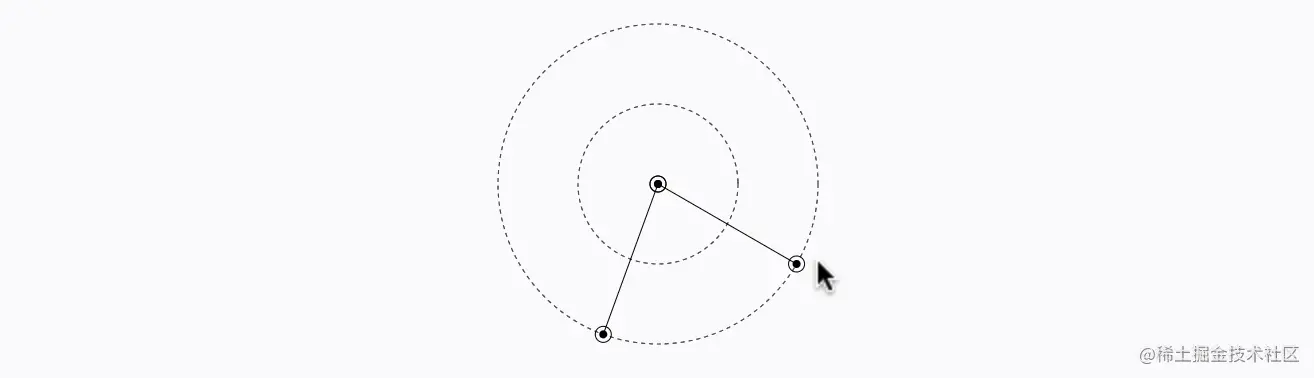
1. 扇形区域的定义

首先来明确一下扇形区域的表示&＃xff0c;如下图所示&＃xff0c;一个 扇形区域 通过五个属性进行描述&＃xff1a;

这里通过 SectorShape 类对扇区的属性进行维护&＃xff0c; 定义如下&＃xff1a;

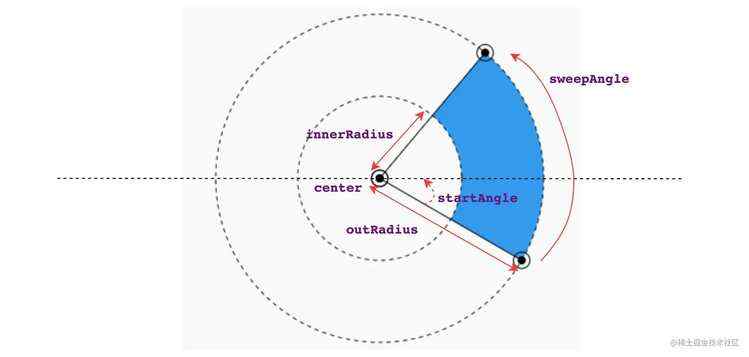
class SectorShape
Offset center; // 中心点
double innerRadius; // 小圆半径
double outRadius; // 大圆半径
double startAngle; // 起始弧度
double sweepAngle; // 扫描弧度
SectorShape(
required this.center,
required this.innerRadius,
required this.outRadius,
required this.startAngle,
required this.sweepAngle,
);


2. 绘制扇形区域

接下来看一下如何绘制扇形区域&＃xff0c;思路是先生成 区域路径 &＃xff0c;然后绘制路径。在生成路径的过程中&＃xff0c;需要知道四个端点的坐标&＃xff0c;如下所示&＃xff1a;

根据 SectorShape 的属性&＃xff0c;可以很轻松地计算出四点的坐标&＃xff0c;如下所示&＃xff1a;其中 shape 是 SectorShape 类型对象&＃xff1a;

double startRad &＃61; shape.startAngle;
double endRad &＃61; shape.startAngle &＃43; shape.sweepAngle;
double r0 &＃61; shape.innerRadius;
double r1 &＃61; shape.outRadius;
Offset p0 &＃61; Offset(cos(startRad) * r0, sin(startRad) * r0);
Offset p1 &＃61; Offset(cos(startRad) * r1, sin(startRad) * r1);
Offset q0 &＃61; Offset(cos(endRad) * r0, sin(endRad) * r0);
Offset q1 &＃61; Offset(cos(endRad) * r1, sin(endRad) * r1);


下面是通过四点形成扇形区域路径的过程&＃xff0c;其中 arcToPoint 能做出指定终点的圆弧路径&＃xff0c;详细介绍可免费参见 &＃xff1a; 《妙笔生花-第五章》 相关方法。

Path path &＃61; Path()
..moveTo(p0.dx, p0.dy)
..lineTo(p1.dx, p1.dy)
..arcToPoint(q1, radius: Radius.circular(r1), clockwise: false)
..lineTo(q0.dx, q0.dy)
..arcToPoint(p0, radius: Radius.circular(r0));


由于 SectorShape 的属性能唯一对应一种扇形区域。 使用为了使用方便&＃xff0c;可以在 SectorShape 中提供一个 formPath 来生成路径&＃xff1a;另外要注意&＃xff0c;需要根据 sweepAngle 的正负确定顺时针与否&＃xff1b;根据 sweepAngle 是否大于 pi &＃xff0c;确定区分取大弧。最后&＃xff0c;根据 center 坐标对路径进行平移操作。

---->[SectorShape#formPath]----
Path formPath()
double startRad &＃61; startAngle;
double endRad &＃61; startAngle &＃43; sweepAngle;
double r0 &＃61; innerRadius;
double r1 &＃61; outRadius;
Offset p0 &＃61; Offset(cos(startRad) * r0, sin(startRad) * r0);
Offset p1 &＃61; Offset(cos(startRad) * r1, sin(startRad) * r1);
Offset q0 &＃61; Offset(cos(endRad) * r0, sin(endRad) * r0);
Offset q1 &＃61; Offset(cos(endRad) * r1, sin(endRad) * r1);
bool large &＃61; sweepAngle.abs() > pi;
bool clockwise &＃61; sweepAngle > 0;
Path path &＃61; Path()
..moveTo(p0.dx, p0.dy)
..lineTo(p1.dx, p1.dy)
..arcToPoint(q1, radius: Radius.circular(r1), clockwise: clockwise, largeArc: large)
..lineTo(q0.dx, q0.dy)
..arcToPoint(p0, radius: Radius.circular(r0), clockwise: !clockwise, largeArc: large);
return path.shift(center);


这样就可以很轻松的通过 SectorShape 对象&＃xff0c;来展示一个扇形区域。其中你可以通过操作 Paint 画笔&＃xff0c;来实现更多的效果&＃xff1a;比如使用的 shader 在扇形区域内填充图片、渐变等&＃xff0c;这些基础可参见小册。

填充颜色	填充图像1	填充图像1

Paint paint &＃61; Paint()
..style &＃61; PaintingStyle.stroke
..color &＃61; Colors.blue
..strokeWidth &＃61; 2;
SectorShape shape &＃61; SectorShape(
center: Offset(size.width / 2, size.height / 2),
innerRadius: 40,
outRadius: 80,
startAngle: 30 * pi / 180,
sweepAngle: -80 * pi / 180,
);
canvas.drawPath(shape.formPath(), paint);


3. 扇形区域的点击校验

下面来思考一个问题&＃xff1a;当手指或鼠标点在界面上&＃xff0c;如何校验该点是否在 扇形区域 之内。如下图&＃xff0c;很明显 p1 在其中&＃xff0c;p2 不在。如何通过代码进行校验呢&＃xff1f;

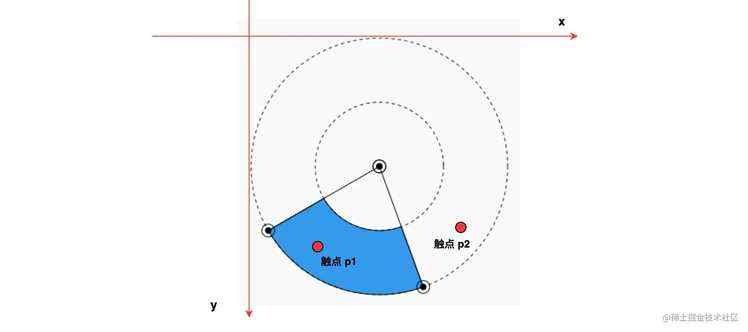
其实&＃xff0c;思路很简单&＃xff0c;点落在扇心区域内&＃xff0c;需要满足两个条件&＃xff1a;

[1]. 扇心与落点的距离 d 在 [innerRadius,outRadius]。
[2]. 扇心与落点的夹角在 [startAngle,startAngle&＃43;sweepAngle] 之间。


由于扇形区域的信息都存储在 SectorShape 类中&＃xff0c;所以可以在其中定义 contains 方法&＃xff0c;用于校验点是否在扇形区内&＃xff1a;

---->[SectorShape#contains]----
bool contains(Offset p)
// Todo


下面&＃xff0c;来实现如下效果&＃xff0c;在按下时&＃xff0c;落点在扇心区域内时&＃xff0c;区域显示填充色示意&＃xff0c;抬起时恢复&＃xff1a;

校验逻辑如下&＃xff0c;其中 校验环形区域 非常简单&＃xff0c;落点与中心距离算出来比较一下即可。如果不再环中&＃xff0c;就可以立刻判定为失败并返回。关于角度的校验&＃xff1a;逆时针扫描时&＃xff0c;终点小于起点&＃xff1b;顺时针扫描时&＃xff0c;终点大于起点&＃xff1b;所以要根据 sweepAngle 区分判断&＃xff1a;

---->[SectorShape#contains]----
bool contains(Offset p)
// 校验环形区域
double l &＃61; (p - center).distance;
bool inRing &＃61; l <&＃61; outRadius && l >&＃61; innerRadius;
if (!inRing) return false;
// 校验角度范围
double a &＃61; (p - center).direction;
double endArg &＃61; startAngle &＃43; sweepAngle;
double start &＃61; startAngle;
if(sweepAngle > 0)
return a >&＃61; start && a <&＃61; endArg;
else
return a <&＃61; start && a >&＃61; endArg;



这样在绘制时&＃xff0c;只要通过下面 tag1 处代码&＃xff0c;使用 shape.contains 方法&＃xff0c;就能校验 p 点是否在扇形区内&＃xff0c;如果在&＃xff0c;则绘制扇形填充。核心的逻辑就是这些&＃xff0c;想看详细的效果可参见源码&＃xff1a; 【sector/02】

---->[Paper#paint]----
SectorShape shape &＃61; SectorShape(
center: Offset(size.width / 2, size.height / 2),
innerRadius: 40,
outRadius: 80,
startAngle: 30 * pi / 180,
sweepAngle: 280 * pi / 180,
);
bool contain &＃61; shape.contains(p); // tag1
if(contain)
canvas.drawPath(shape.formPath(), paint);
Paint paint2 &＃61; Paint()..style&＃61;PaintingStyle.stroke;
canvas.drawPath(shape.formPath(), paint2);


4. 几何校验与 Path 校验的区别

有些聪明的小伙伴可能会问&＃xff1a;

能问出这个问题&＃xff0c;说明对绘制的基础掌握的还是比较牢固的。Path#contains 方法对于不规则的图形校验是至上法宝。但对于标准图形&＃xff0c;通过几何方法进行校验比较简单&＃xff0c;就像到楼下超市买瓶饮料&＃xff0c;没必要开车去买。

为此&＃xff0c;我做了一个小测试&＃xff0c;看看两者在 百万次校验下的表现。如下 tag1 是使用 Path 判断&＃xff0c;tag2 是上面基于几何型的判断。进行了两组四项测试&＃xff0c;表现如下&＃xff1a;

SectorShape shape &＃61; SectorShape(
center: Offset.zero,
innerRadius: 40,
outRadius: 80,
startAngle: 30 * pi / 180,
sweepAngle: 80 * pi / 180,
);
// Offset offset &＃61; const Offset(112.7, 148.4);
Offset offset &＃61; const Offset(0, 0);
Path path &＃61; shape.formPath();
int time &＃61; DateTime.now().millisecondsSinceEpoch;
for (int i &＃61; 0; i <1000000; i&＃43;&＃43;)
// path.contains(offset); // tag1
// shape.contains(offset); // tag2
int endTime &＃61; DateTime.now().millisecondsSinceEpoch;
print(&＃39;$endTime - timems&＃39;);


可以看出通过几何形的判断要快一些&＃xff0c;这也是最直接的方式。当初步校验不合格&＃xff0c;可以直接结束判断&＃xff0c;而且其中只是基本的运算符计算&＃xff0c;没有涉及复杂的循环判断。对于标准图形来说&＃xff0c;这种方式既有效&＃xff0c;又便捷&＃xff0c;是比较好的。

但千万别会错意&＃xff0c;我并不是说 path.contains 方法耗时&＃xff0c;百万次才耗时两三百毫秒&＃xff0c;如果不是超大批量的路径遍历校验&＃xff0c;基本上也没什么影响。一般界面上同时校验几十个路径就顶天了&＃xff0c;所以也不用担心&＃xff0c;就像一秒赚几百万&＃xff0c;不必要为丢了一毛钱而忧心忡忡。

到这里&＃xff0c;扇形区域路径的获取、绘制与点击校验就完成了。对于 饼状图 而言&＃xff0c;相当于最基础的材料已经准备完毕。下一篇&＃xff0c;将基于本文的扇形区域&＃xff0c;简单实现一个 饼状统计图 。那本文就到这里&＃xff0c;谢谢观看 ~

更多 Flutter 绘制技巧&＃xff0c;欢迎关注 《Flutter 绘制探索》 专栏。

最后

如果想要成为架构师或想突破20~30K薪资范畴&＃xff0c;那就不要局限在编码&＃xff0c;业务&＃xff0c;要会选型、扩展&＃xff0c;提升编程思维。此外&＃xff0c;良好的职业规划也很重要&＃xff0c;学习的习惯很重要&＃xff0c;但是最重要的还是要能持之以恒&＃xff0c;任何不能坚持落实的计划都是空谈。

如果你没有方向&＃xff0c;这里给大家分享一套由阿里高级架构师编写的《android八大模块进阶笔记》&＃xff0c;帮大家将杂乱、零散、碎片化的知识进行体系化的整理&＃xff0c;让大家系统而高效地掌握Android开发的各个知识点。

相对于我们平时看的碎片化内容&＃xff0c;这份笔记的知识点更系统化&＃xff0c;更容易理解和记忆&＃xff0c;是严格按照知识体系编排的。

全套视频资料&＃xff1a;

一、面试合集

二、源码解析合集

三、开源框架合集

欢迎大家一键三连支持&＃xff0c;若需要文中资料&＃xff0c;可扫描文末CSDN官方认证微信卡片免费领取↓↓↓